Waves 4


	Let us now examine the main properties characterizing a wave. Let us imagine we stand on one side of the ripple tank, our eyes level with the surface of the liquid (supposing the sides of the tank are transparent) and let us observe the profile of the rectilinear waves produced by a planar plate while they propagate. If the vibration generating the waves is regular in time, the surface of the moving liquid shows crests and valleys which also are repeated in regular fashion and can be described by means of charateristic magnitudes.

Animation of plane waves produced in the basin of a ripple tank where the terminal immersed in water oscillates in a regular fashion.

Same situation as above, this time in a frontal view.

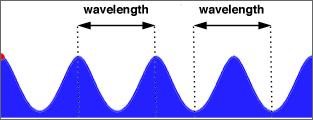
A snapshot taken from the side, with the corresponding wavelength.

The distance between two crests or two valleys is called wavelength. What is its meaning? Let us look at the plate of the ripple tank which oscillates with a constant frequency (the frequency is the number of oscillations per second). At a given time the plate generates a rectilinear crest which propagates on the surface of the water. After a time equal to the duration of one oscillation, the plate generates another crest, which also follows the same path, and so on and so on. Every time a crest is generated, the preceding crest has moved away from the source by a length equal to the distance between two crests, that is a wavelength. Thus the wavelength is the distance walked by the wave during the time in which the source completes one fulll oscillation. The ratio between wavelength and the time of an oscillation, (having the dimension of a velocity) represents the propagation velocity of the wave.

Let us imagine now that we increase the oscillation frequency of the arm of the ripple tank. This way crests and valleys will be produced more rapidly. Since the rate with which the waves moves apart from the plate of the ripple tank stays practically unchanged, the wavelength decreases and the waves become “thicker”. On the contrary, when the frequency of oscillation of the ripple tank is decreased, the wavelength will increase.

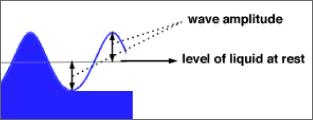
The maximum height (equal to the maximum depth) reached by the liquid with respect to the rest position during the oscillation is called wave amplitude.

Until now, we have taken in consideration the motion of waves, that is of the entire surface of the liquid in which the propagation occurs. Let us now turn to what happens in a given point of the liquid surface when the wave reaches it.

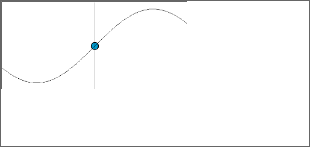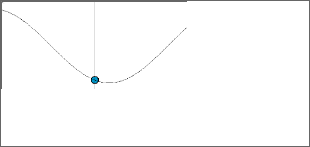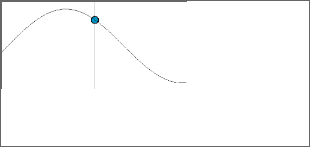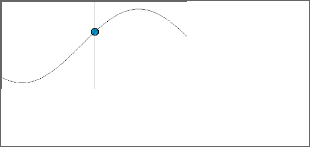
Effect of the passage of the wave through a given point. Let us think of the blue dot as if it were a piece of cork floating on the water surface. The cork oscillates up and down with a frequency equal to that of the vibration of the ripple tank , which is the frequency of the wave.

From what we already said, it is clear that frequency and wavelength are interconnected through the velocity of wave propagation. It is intuitive that if crests and valleys grow thicker (that is if the wavelength decreases) and the velocity of propagation stay the same, our dot oscillates faster (the frequency increases). In general, long waves have low frequency, whereas short waves have high frequency.

The concepts illustrated above apply to all kind of waves, including the electromagnetic waves quoted earlier. For instance, the red light has greater wavelength (and lower frequency) than blue light, X rays have very high frequency and very short wavelength, while radio waves have low frequencies and large wavelengths. The ensemble (also called spectrum) of electromagnetic waves can be also represented as function of frequency or al function of wavelength, as shown in the figure.

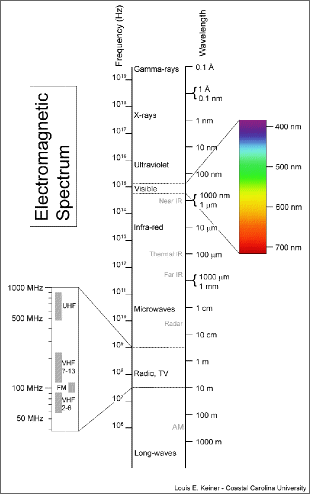
Spectrum of electromagnetic radiation. As explained in the text, electromagnetic radiations exhibit, under given circumstances, wavelike character. The various types of electromagnetic waves are here ordered as function of frequency (left scale) or of the wavelength (right scale). As one can see, the two quantities behave in opposite ways, if one grows the other decreases, and the other way around. The light is but the small visile part of the whole electromagnetic spectrum, which has been expanded indicating the succession of colours corresponding to the perception of the different frequencies and wavelengths. To see an enlarged representation of the spectrum, click on the figure.

click on the image for enlargement

		HOME \| WHAT IS ABOUT \| EXPLANATION \| HISTORY \| BEAUTY \| BACKSTAGE \| THINKING ABOUT \| THE MOVIE \| ABOUT US \| LINKS & BIBLIO \| CONTACT