 |
|||||||||
|
|||
|
|||||||||||||||||||
 |
|||||||||||||||||||
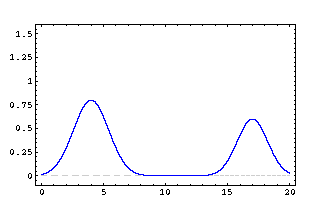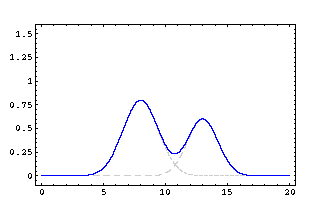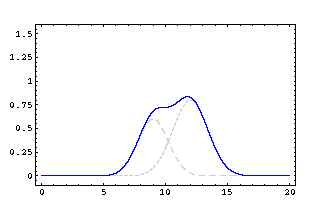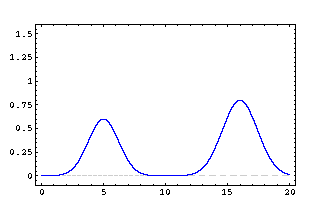
Two wave perturbations moving in opposite directions on the same string. In this case both produce shifts of the string in the same direction (upward) with respect to the position of the string at rest. The waves interlace one another without being disturbed. In the moment in which they cross and superimpose, the shift of the string is determined by the sum of the amplitudes derived, at each given moment, by the single waves. In the moment in which two crests cross the same point of the string, the latter is subject to a shift due to the sum of the amplitudes of the two waves. Animation courtesy of Dr. Dan Russell, Kettering University |
|||||||||||||||||||
|
|||||||||||||||||||
|
 |
|
|||||||||||||||||
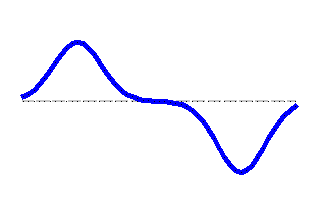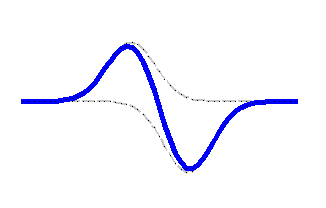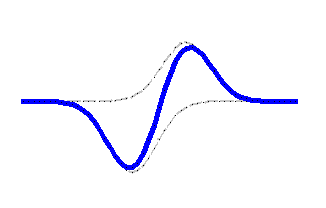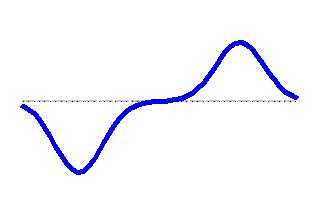
Similar example, in which the two waves have equal shapes, but produce shifts upward in one case, downwards in the other. In this instance, at the moment in which the two waves are exactly superimposed, all points in the superposition area are subject to contrasting shifts, so that the algebraic sum is null and the string stays put in the rest position. Animation taken from the site http://www-1.unipv.it/grando/ondeweb/esempio%20sovrapposizione.htm |
|||||||||||||||||||
|
|||||||||||||||||||
|
||||||
HOME | WHAT IS ABOUT | EXPLANATION | HISTORY | BEAUTY | BACKSTAGE | THINKING ABOUT | THE MOVIE | ABOUT US | LINKS & BIBLIO | CONTACT |
||||