HOME | WHAT IS ABOUT | EXPLANATION | HISTORY | BEAUTY | BACKSTAGE | THINKING ABOUT | THE MOVIE | ABOUT US | LINKS & BIBLIO | CONTACT

Let us keep considering a ripple tank in which two periodic circular wave trains are generated by using two tips connected to a single vibrating staff. The moment when the staff starts vibrating, the two tips start the generation of waves. Let us consider on the liquid surface the points equidistant from the sources. The two perturbations which at a given time reach every one of these points are going to be always equal (in particular at a given time they will correspond to two crests or two valleys) and as a consequence, owing to the superposition principle, the shift of the point from the equilibrium position will be at each instant twice as large as if only one source existed. The points oscillate with an amplitude twice as large as that of single waves.

What happens in the other points on the surface of the liquid ? The outcome depends on the difference between the distances of the point considered from either source.

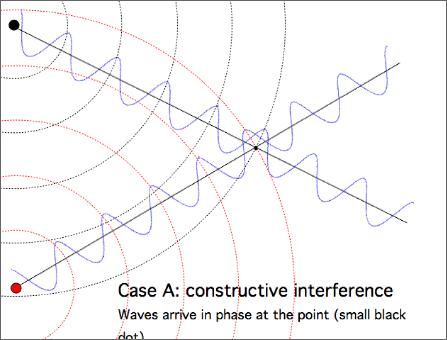
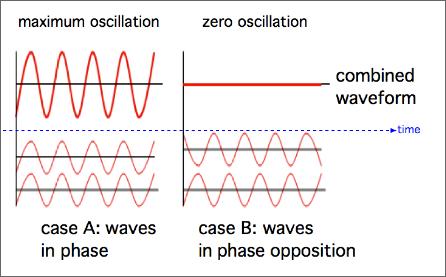
In the case in which such difference equals an integer number of wavelengths, once more the perturbations coming from the sources at a given instant are going to be in phase (in partcular at a given time there will be two crests, at another two valleys). The points corresponding to this situation are going to oscillate with an amplitude equal to the sum of the amplitudes of the two waves, (such amplitudes can be considered almost equal until the difference between the distances of the point examined from both sources is small enough).

In the cases hitherto considered we say that the waves arrive “in phase” and we talk about “constructive interference” (see the figure below depicting case A).

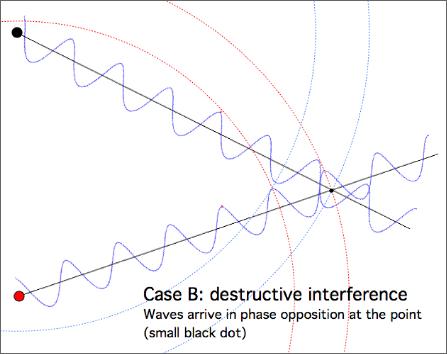
In the case in which the difference between the distances of the point from either source equals an half wavelength, or rather an odd number of half wavelengths, the perturbations reaching at the same time from the two sources correspond to motions in opposite directions (in particular at a given instant one crest and one valley will be superimposed). We say that in these points the waves arrive in phase opposition. And we define this “destructive interference” (see the figure below depicting case B). If we can consider equal the amplitudes of the opposite shifts which would be caused by each sources, these points would be invariably at rest. These points define the “nodal lines”.

In the points in which the difference in distance from the sources is braketed between two sequential numbers of half wavelengths, the perturbations started in either source do not reach a given point in phase nor in phase opposition but amplitude oscillations ensue depending on the position of the point.

Case A: Constructive interference. We imagine to take a snapshot in order to see what happens in a given point (the black dot) reached by waves coming from two coherent sources (the two larger dots, one black and one red, on the left side of the drawing). With the dashed circles we have here pointed out the crests of the waves coming from the two sources. The two blue lines represent the level of the liquid we would have along the paths evidenced by the black straight lines, if one only source was present. We notice that, in the moment chosen for the snapshot, in the point where the black lines cross, both waves exhibit a crest. In this case the two perturbations act both in the sense of raising the liquid: the effects reinforce one another, so that the rsulting wave shows a crest of height twice that expected from a single source. This happens in all the points in which the circles representing the crests of the two waves cross one another.

Case B: Destructive interference. The snapshot is taken at the same time as the one above. This time, for the first source (the black one) we use blue circles to identify, not the crests, but the valleys. Here we focus on one point in which the wave coming from the red source has a crest, as was the case in the example above, while the wave coming from the black source shows a valley. In this case the two perturbations (one tending to raise the liquid, the other tending to lower it) cancel one another and the liquid stays put.

The figure shows a plot in which the variation with time (direction of the blue arrow) of the level of the liquid oscillates in time with the same frequency of the interfering waves, but with an amplitude given by the sum of the amplitudes of the single waves. In the case of opposing phases the liquid stays put at the rest level.

Even though the sources do not vibrate in phase to one another, as long as they generate periodic waves and have the same frequency, so that there is a constant delay between the production of crests and valleys by one source and that by the other (we say that the waves have a constant phase difference), one has an interference pattern, only the nodal lines are shifted.